物理学の世界には、ニュートン力学や波動、電磁気学など様々な分野がありますが、それらは概ね19世紀に確立された分野であり、
これを古典物理学と呼びます。
対して、20世紀以降に新しく生まれた物理学(特に量子力学)を現代物理学
と呼びます。そのため、物理学では「古典的」の対義語として「量子的」という表現をします。
この量子力学では、私たちの感覚とはあまりにもかけ離れた、とても不思議な現象が数多く存在します。
その中でも最も象徴的なのが『量子もつれ(量子エンタングルメント)』であり、
1909年にアインシュタインが「光子の非局所性」を提唱して以来、『物理学の100年論争』として波紋を呼んできました。
この記事では、そんな量子もつれについてなるべく簡単に、わかりやすく、順を追って解説していきます。
※量子力学は、その不思議さ故にスピリチュアルや霊感商法などの用語としてしばしば悪用されますが、
これから解説するような内容はあくまで量子のような非常にミクロな世界でのみ起こる現象であり、
私たちの目に見える形で現れるものではないということに注意してください。
1. 量子力学とは?
まず、そもそも量子力学とはどんな分野なのかを解説していきます。
古典力学(ニュートン力学)では私たちの身の周りにある物体の運動や力、例えば車や野球ボールのような物の運動を記述します。
しかし分子や原子といったミクロな世界ではこの古典的な運動法則が通用せず、私たちの想像とは全く違う振る舞いをするのです。
物質は分子や原子から成っていることはご存知でしょう。
そして原子はさらに陽子・中性子に、陽子・中性子はさらにクオークと呼ばれる素粒子に分解できます。
素粒子とは物質を構成する最小単位であり、電子や光子などもこれに含まれます。
量子力学とは、原子や素粒子のようなミクロな世界を記述する力学であり、このような非常に小さな粒子を量子と呼びます。
量子力学では古典的な考え方では説明のつかない不思議な現象がたくさん存在しますが、
まず量子の特徴として押さえておかなければならないのが、「不確定性」という性質を持っているという点と、
「粒子性」と「波動性」の両方を持っているという点です。
そしてこれらの性質こそが私たちを混乱させ、量子力学を難しくする根元なのです。
ではそれらは一体どのようなものなのでしょうか。
2. 光の非局所性と100年論争
量子力学が大きく発展するようになったきっかけとも言える現象「光の非局所性」を提唱したのが、天才アインシュタインでした。
物理学における「局所性」とは、ある地点で起こった現象によって、その影響や情報が離れた地点へ直ちに伝わることは無いという性質のことです。
つまり「非局所性」とは、直ちに離れた地点へ情報が伝わってしまうということを表しています。
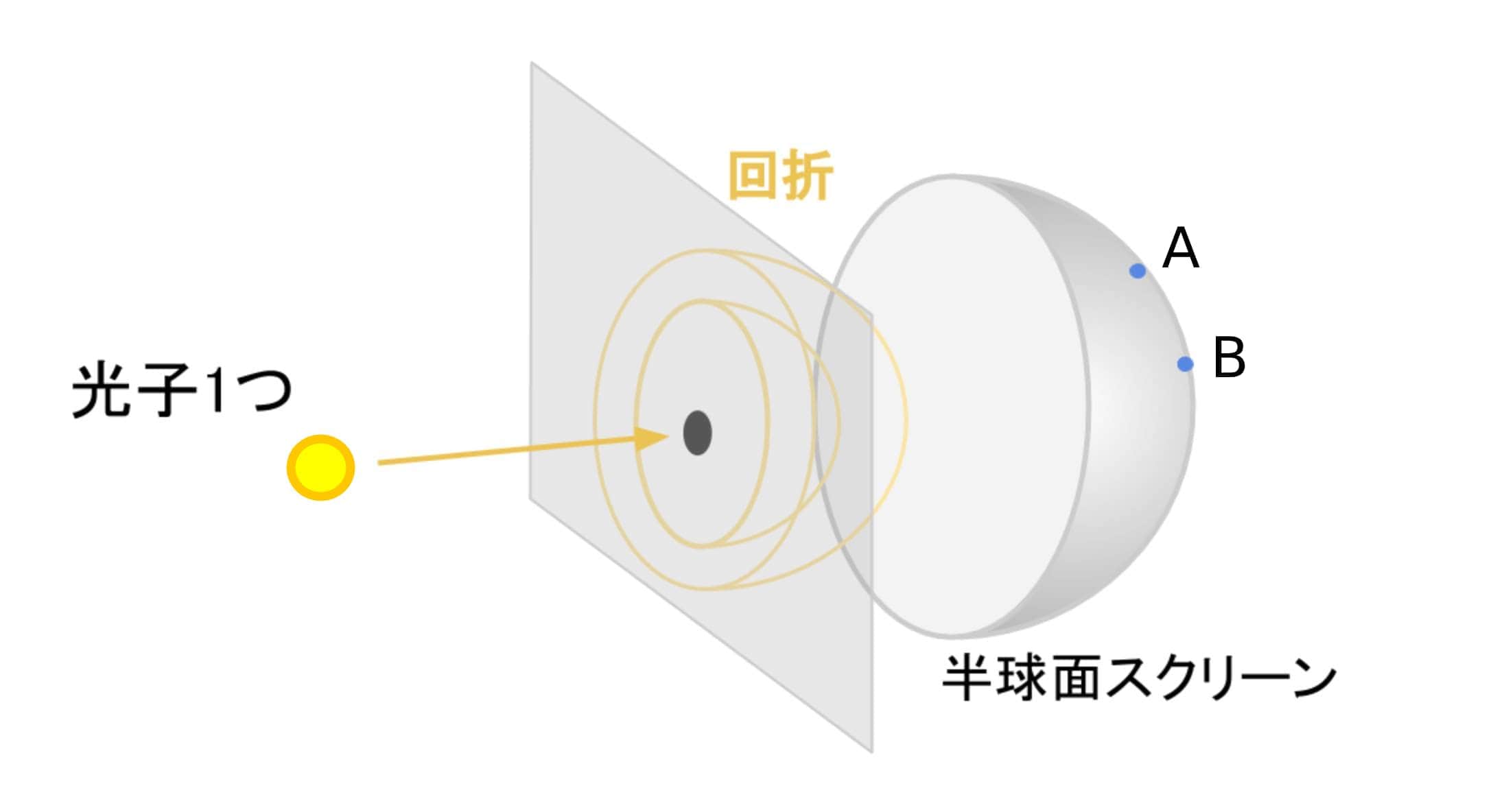
上図のように単一光子を放射し、光子がピンホールを通過すると回折し放射状に広がります。(波動性)
スクリーンに到達する直前まではスクリーン上の全ての点に確率的に光子が存在しているはずです。
しかしこれがスクリーンに到達すると必ず1点でのみ観測され、点Aと点Bのような複数点で同時に検出されることはないのです。(粒子性)
「ピンホールを通り回折した単一光子は空間的に広がるが、異なる2点で同時に観測されない。」
この状況に対し約100年前アインシュタインは、「ある場所で観測された影響が他の離れた場所に及ぶような
奇妙な相互作用(spooky action at a distance)が存在するのではないか」と主張しました。
そしてこの「量子の非局所性」はその後100年間、物理学の謎として議論されることとなったのです。
3. 不確定性原理と重ね合わせ
量子力学といえば、不確定性原理という言葉を聞いたことがある人は多いでしょう。
これ自体はそれほど難しい話ではありません。下図を見てみましょう。
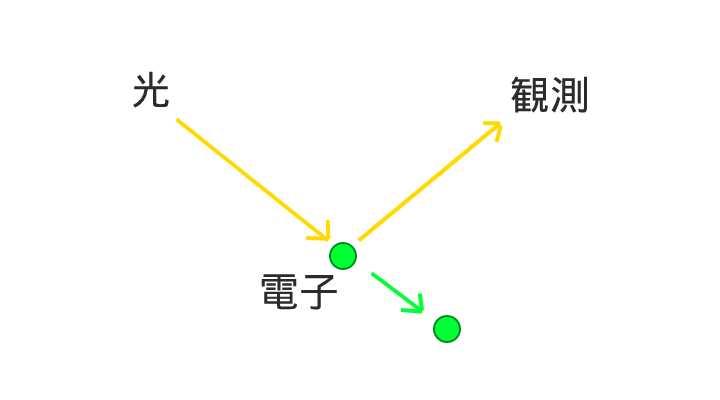
図のようにガンマ線を電子に当ててその位置を測定する場合を考えます。
この時、電子は光の影響を受けて運動が変わってしまいます。
位置の特定を正確にしようとすればするほど、照射する光のエネルギーを大きくしなければならず、電子が受ける影響も大きくなってしまいます。
つまり運動量が不確かになります。
これは量子力学の基本原理であり、1927年ハイゼンベルクによって導かれ、以下の式で表されます。
ハイゼンベルクの不等式
ΔxΔp ≥ ħ/2
Δx = (位置の不正確さ)、Δp = (運動量の不正確さ)
ħ (ディラック定数、エイチバー) = (プランク定数 h / 2π)
これは何かというと、「位置のあいまいさと運動量のあいまいさを掛けた値が、ある値よりも小さくなる事はない」、
つまり「量子の位置と運動量の両者を正確に測定し、決定することはできない」ということを意味しています。
もう少し具体的に言うと、Δx(位置のあいまいさ)が0に近づくほど(つまり位置が正確に決まるほど)、
Δp(運動量のあいまいさ)が∞無限大へ近づく(つまりどう動いているかがわからなくなる、どんどんあいまいになる)ということです。
(プランク定数は非常に小さい(10の-34乗)とはいえ、0ではないため)
ここまでの話だと、あくまでこれは観測技術的な話であって、量子の特性と言えるのか?という気がしてきます。
しかしこれが量子の特性であると考えられる例を以下に挙げてみます。
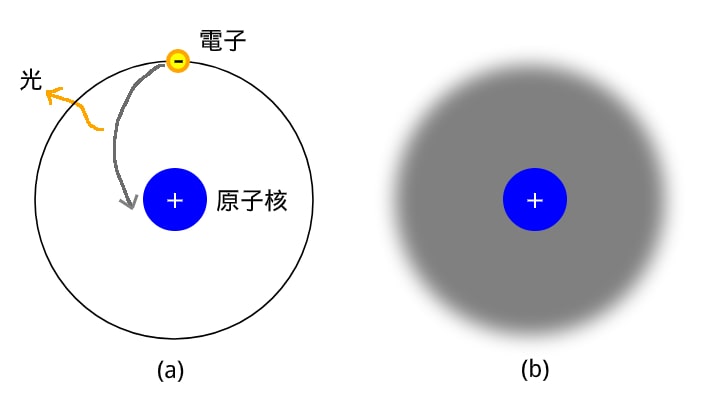
中高の理科では水素原子は図(a)のように、原子核(陽子1つ)のまわりを電子1つが回っていると教えられました。
しかし本当にこのように負の電荷を帯びた電子が円運動をすると、電磁誘導により電磁波を放出するはずです。
そうすると電子はその分だけエネルギーを失い、原子核へ落ちていくことになります。
電子が原子核へ落ちていくと、電子の存在範囲がどんどん狭まっていく(Δxが0に近づく)ため、運動量の不確かさが大きくなっていきます。
つまり電子の速度やエネルギーのとりうる範囲が広がるため、もし電子が完全に原子核へ落ちてしまうとエネルギーが無限大を許してしまい、これは現実的には起こり得ません。
実際、水素原子はエネルギーを放出することなく安定的に存在しています。
ではどのように解釈すればいいのでしょうか。
量子力学では電子は図(b)のように、位置や運動量といった物理量が「あいまいに」決まっている状態で「雲」のように存在していると考えます。
この電子雲のように、電子はその存在領域内のあらゆる位置にいる「状態の重ね合わせ」として存在しており、原子核の周りを回っているわけではないため水素原子は電磁波を発生せずに安定存在しているという解釈です。
まとめると、不確定性原理により電子は原子核へ落ちることなく、状態の重ね合わせとして存在するためエネルギーを失うことなく安定的に存在しているのです。
この「重ね合わせ」という概念が想像し難いと思うのですが、量子が複数存在しているのではなく、1つの量子が様々な位置にいる状態が重ね合わさっているということです。
このような概念から「多世界解釈」のような理論が派生して生まれています。
他にも、不確定性原理の影響が顕著に表れる例として「零点振動」というものがあります。
これは、量子は絶対零度(−273度)下においても、
不確定性原理によって完全に静止(ΔxもΔpも0)することなく僅かに振動する(零点エネルギーを持つ)という現象です。
これによってヘリウムは絶対零度付近でも固化しないといいます。
これらの例からも、不確定性原理は量子のもつ性質であるということは納得できるかと思います。
※ちなみに近年、ハイゼンベルク不等式の改良版が導出され、これが実証されています。(ハイゼンベルク不等式の破れ)
「小澤の不等式」と呼ばれ、ハイゼンベルクの式よりも右辺の値が小さくなっています。
つまりもっと正確に測定する事が可能だという事が確かめられています。
4. 量子もつれの発見 - EPRパラドクス
ここまで、量子力学は「不確定性原理」や、そこから導き出された「状態の重ね合わせ」を基本原理としていることを説明してきました。
これらの原理の下に、1930年ごろにかけて量子力学は盛んに研究されていましたが、
1935年にアインシュタインはポドルスキー、ローゼンと共に量子力学の「不完全さ」を示す論文を発表し、
3名のイニシャルを採って「EPRパラドクス」と呼ばれるようになりました。
(Can quantum-mechanical description of physical reality be considered complete? - 物理的実在の量子力学的記述は完全だとみなせるか?)
先述した通り、 量子論においては観測するまではその量子の状態を一意に決めることはできませんでした。(非実在性)
しかしアインシュタインは、次のような2量子の系について思考実験を行いました。
過去に相互作用したことのある2粒子、つまり「位置の和(距離)」と「運動量の和」が確定している2粒子A、Bがあると仮定します。
(この2粒子のような関係を「量子もつれ(量子エンタングルメント)」と呼びます。)
ここで、Aの位置を測定すると、Bとの距離はわかっているため、Bの位置はBに何の操作をすることもなく確定してしまいます。
運動量についても同様に、Aを測定すれば自動的にBも確定してしまいます。
つまり粒子Bについて、位置も運動量も観測する前から決定することができる(実在する)ため、
量子論の「観測するまでは状態を決めることはできない」という波動関数の記述は不完全であると結論づけたのです。
この論文は物理学会に大きな反響を生み、シュレーディンガーもこれに同調し、
量子論が正しいなら「量子もつれ状態の遠く離れた2粒子間で情報が光速を超えて瞬時に(非局所的に)伝わる」ことになってしまい、
また「箱の中の猫は開けるまでは生きている状態と死んでいる状態の重ね合わせ状態である」というようなばかげたこと(シュレーディンガーの猫)すら考えられる
と量子論に疑問を呈しました。(Die gegenwärtige Situation in der Quantenmechanik)
これらの主張に対しボーアは、
地点Aでその位置を観測したとしても、地点Bにおいてはその事実を知る術がなく、従来の光速以下の情報伝達手段で伝えるしかないため、その局所性が破れることはない
と反論しました。
アインシュタインが波動関数を「不完全である」としたのは、それを否定するつもりだったのではなく、
ある地点で起きた現象によって別のある地点へ影響を与えるような未知の「隠れた変数」が存在しているのではないかと考えていたためです。
しかしそれを見つけることは最期まで出来ませんでした。
そしてついに1964年、アインシュタインの予想したような隠れた変数がもし存在するならば満たさなければならない不等式「ベルの不等式」
が成立しないことが実験によって証明されてしまいました。(ベル不等式の破れ)
これによって量子論においては、その
非実在性(量子の状態は観測するまではわからない)や非局所性(ある地点で観測した影響が直ちに他の地点へ伝わる)を認めざるを得なくなったのです。
5. EPRペアの生成
量子もつれの関係にある量子ペアのことをEPRパラドクスにちなんでEPRペアと言います。
さて、それでは実際にそのようなEPRペアはどのように生成できるのでしょうか。
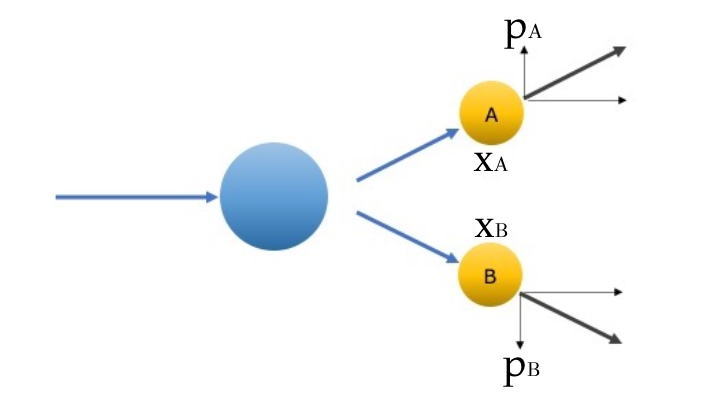
イメージとしては、下図のように1つの量子が2つに分裂してくれるのが最もわかりやすいでしょう。
この図では、A,Bのx方向の距離(xA - xB)も、y方向の運動量の和(pA + pB)も0となり、もつれ状態になっています。
では実際に、光子でこのようなEPRペアを生成する方法を一つ紹介します。
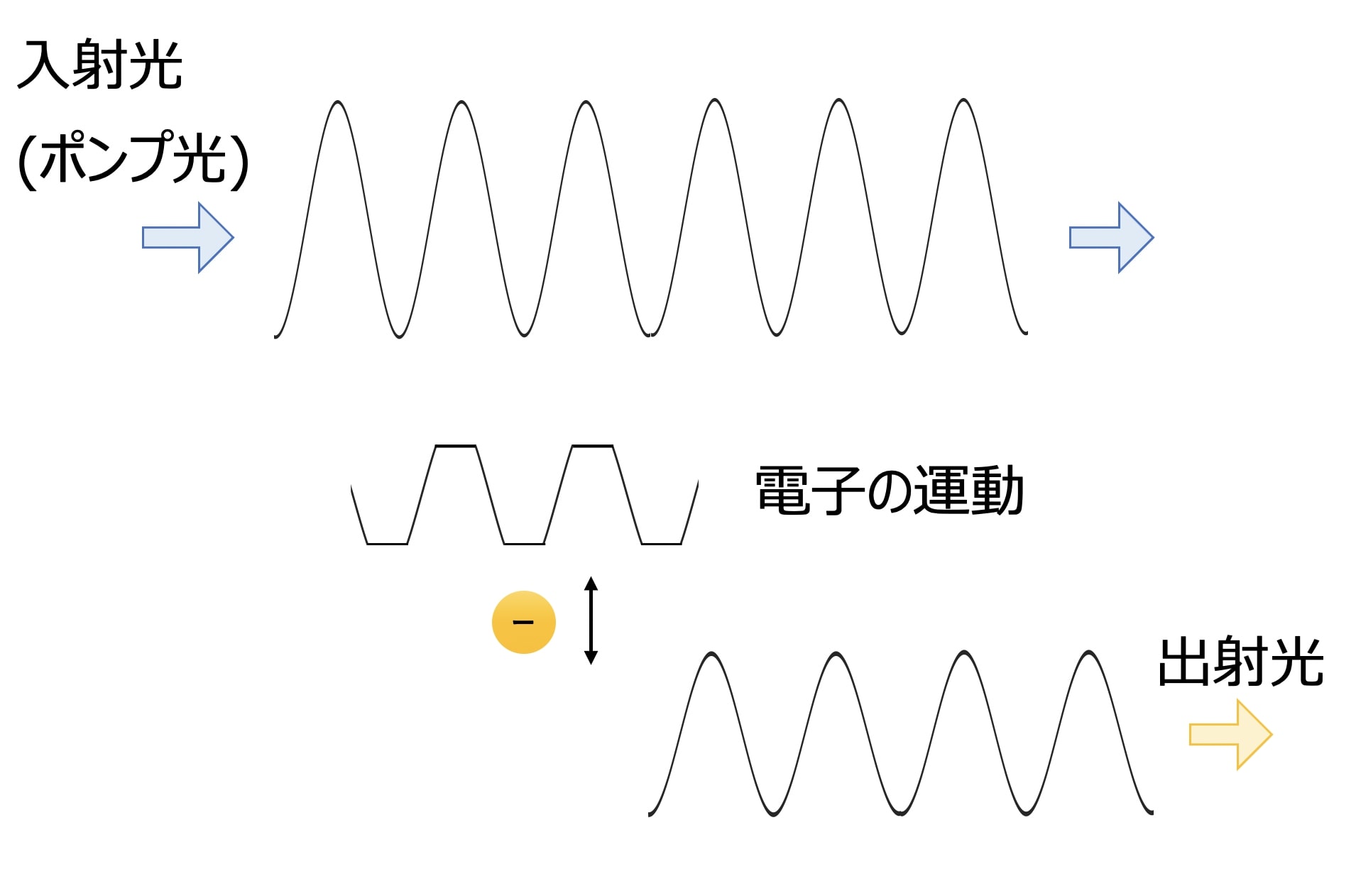
まず、下図のように光が透明な物質に入射する場合を考えてみます。
このとき、物質中の電子は入射光の電場により力を受け振動し、振動した電子の電磁誘導により電磁波を発生します。
また、電子の存在領域は限られているため、図のように強度の高い光(ポンプ光)を入射すると電子の運動は複雑(非線形)になります。
(可動域の限界を超えて力を受けている間は静止する)
そのため出射光も複雑な形となります。(図では簡単にしてありますが)
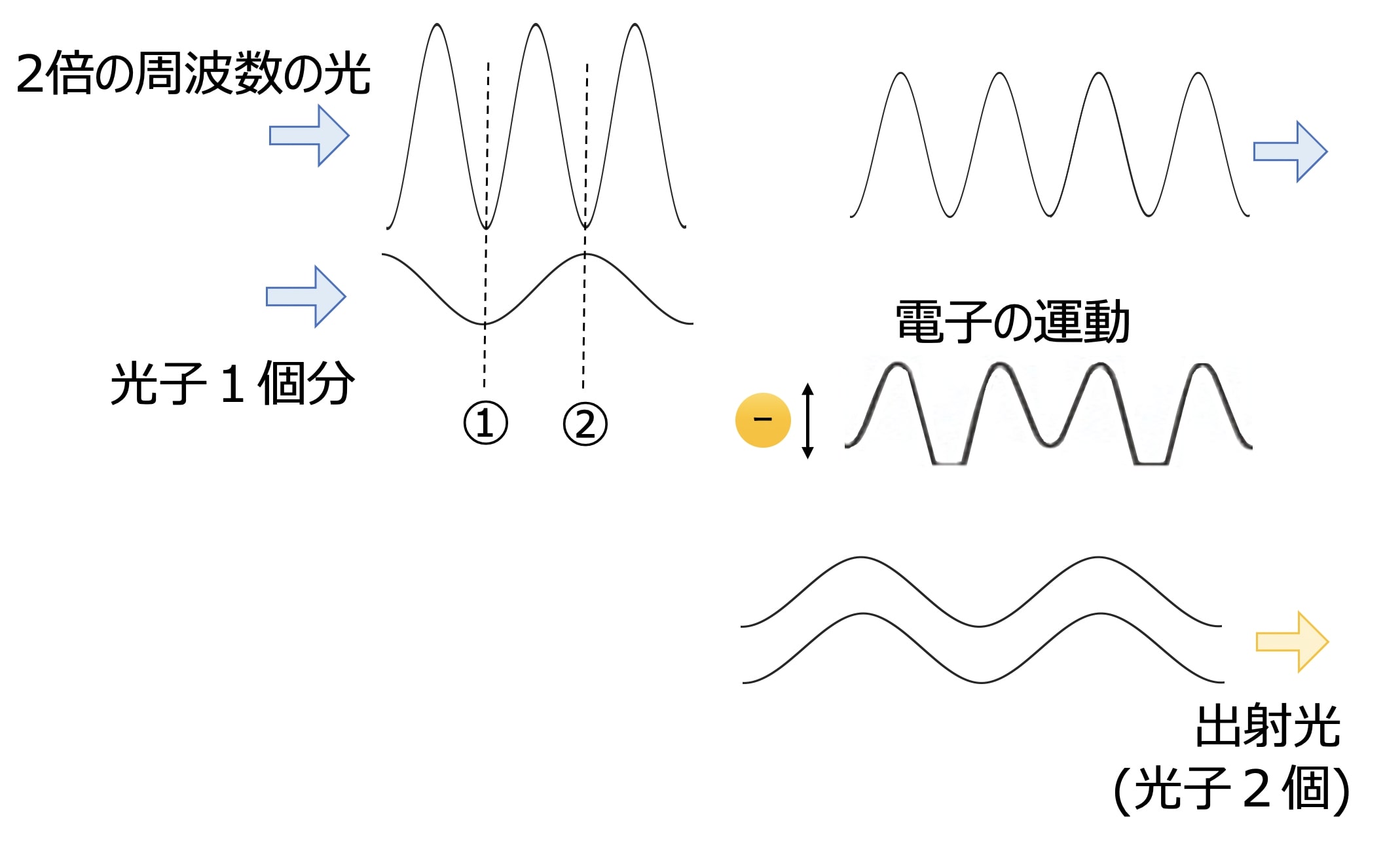
次に、下図のように光子1個分の弱い光と、光子の2倍の周波数となる光を入射した場合について考えてみます。
この2つの光が干渉すると、周期ごとに①強め合ったり②弱め合ったりするため複雑な形のポンプ光となります。
この強め合うタイミングで電子の運動も大きくなり、先ほどと同様に複雑な動き(非線形)となります。
この周期は2倍の周波数の光の半分になるので、光子1つの入射光と同じ周波数の光が発生することになります。
また、そのエネルギー源は2倍の周波数の光なので、結果として出射光は2倍の周波数の光が少し弱まり、入射した光子が2個に増えることになります。
(量子は1個や2個といった単位でしか存在できないため、光子が増幅されるには2個になるしかない)
ここで少し話を戻して、先述した「零点振動」とは、真空場においてもエネルギーは0とはならず、「ゆらぎ」のような状態であるというものでした。
実は下図の入射光の光子1個については、この「ゆらぎ」が入射したとみなすことができ、
実際には何も入射させる必要はなく、ポンプ光(2倍の周波数の光)のみ入射させればよいのです。
(つまりポンプ光の光子1個が半分の周波数の光子2個に分裂したとも言えます)
そして、このような非線形光学現象による光生成過程を「光パラメトリック過程」と呼びます。
このようにして生成した光子対は、1つの光子が2つの光子A、Bに分裂したとみなすことができるため、
運動エネルギー保存によりそのsin成分は反転しており、cos成分は等しくなります。
つまり (Aのsin成分) + (Bのsin成分) = 0 、かつ (Aのcos成分) - (Bのcos成分) = 0 となるため、光子AとBはもつれ状態となっています。
しかし、AとBは空間的に重なっているためEPRペアとは言えないことに注意が必要です。(sin成分は打ち消し合って観測できない)
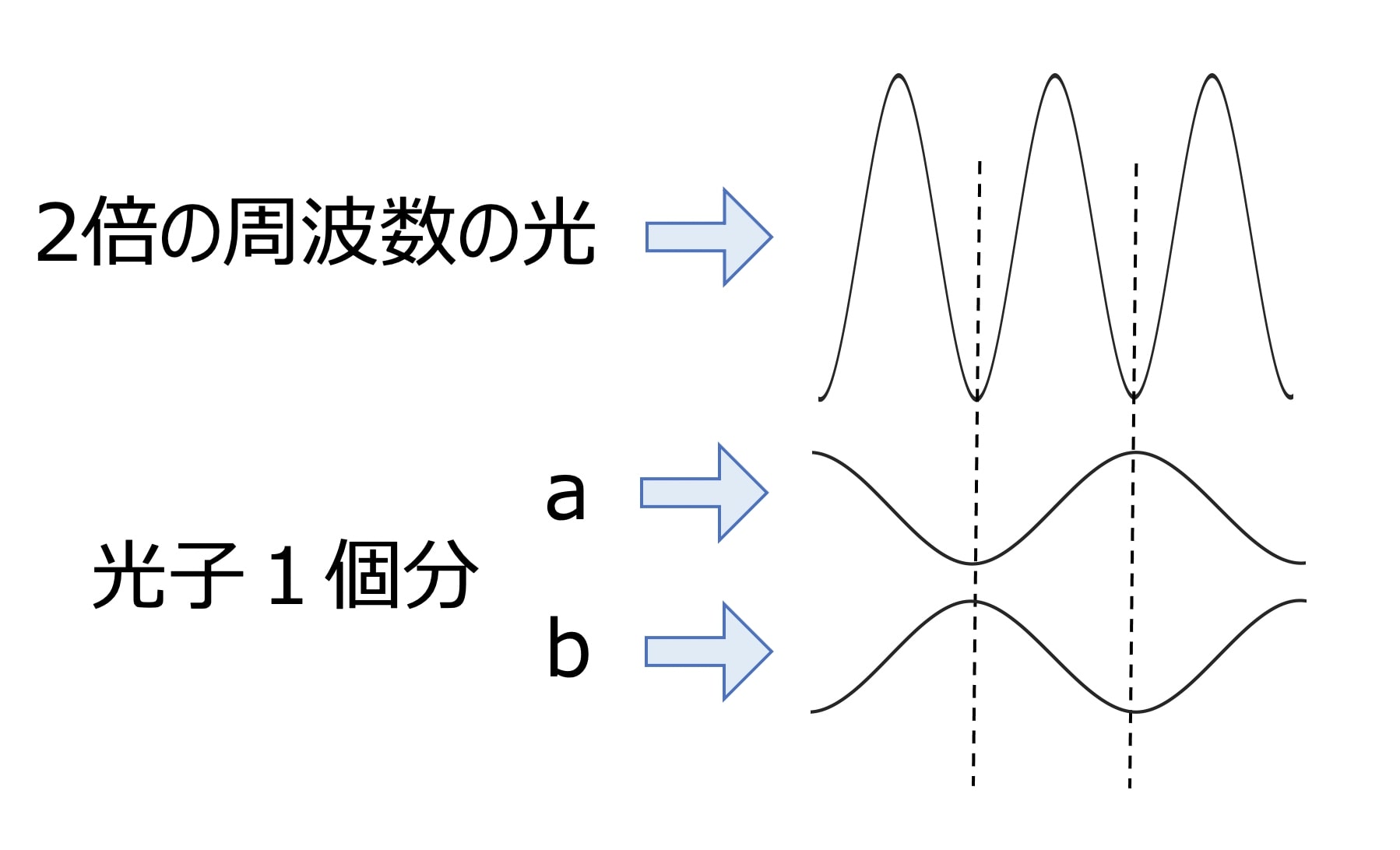
また、上記のような現象が起こるのは、ポンプ光と光子1個の位相が揃う下図のa、bの2通りのみであることがわかります。
(互いに強め合ったり弱め合ったりするタイミング)
またa、bはどちらも真空場なので等しい確率で起こります。
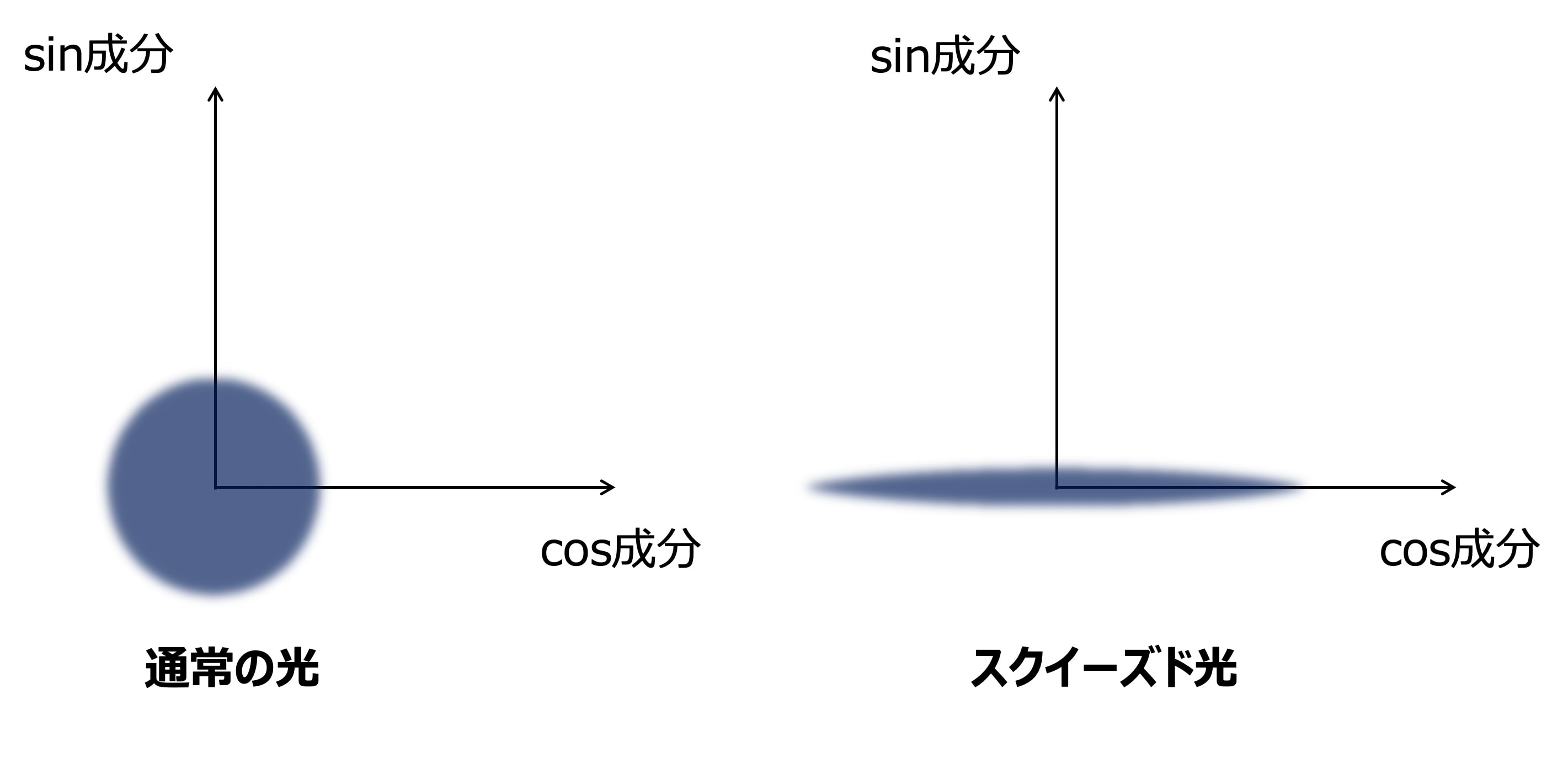
よって、この過程で生成される光は下図の右側のように、振幅のsin成分がなくcos成分が両方向に増幅された状態になります。
これはつまり運動量の不確定性が減少し、位置の不確定性が増幅された特殊な状態と言うことができます。
またこのような光学処理によって不確定性を制御した状態の光を「スクイーズド光」と呼びます。
言うまでもなくこれらは量子論から生まれた最先端技術であり、量子コンピュータなど様々なものに応用されています。
さて、ここまでで光子1個を2個に分裂させることはできましたが、スクイーズド光そのままではEPRペアとは呼べず、空間的に離す必要があります。
そのために「ハーフビームスプリッター」と呼ばれる特殊なガラス板を使用します。
その名の通り、光を半分だけ透過し、半分は反射する板です。また、片面だけ反射光の位相が反転するように加工されているとします。
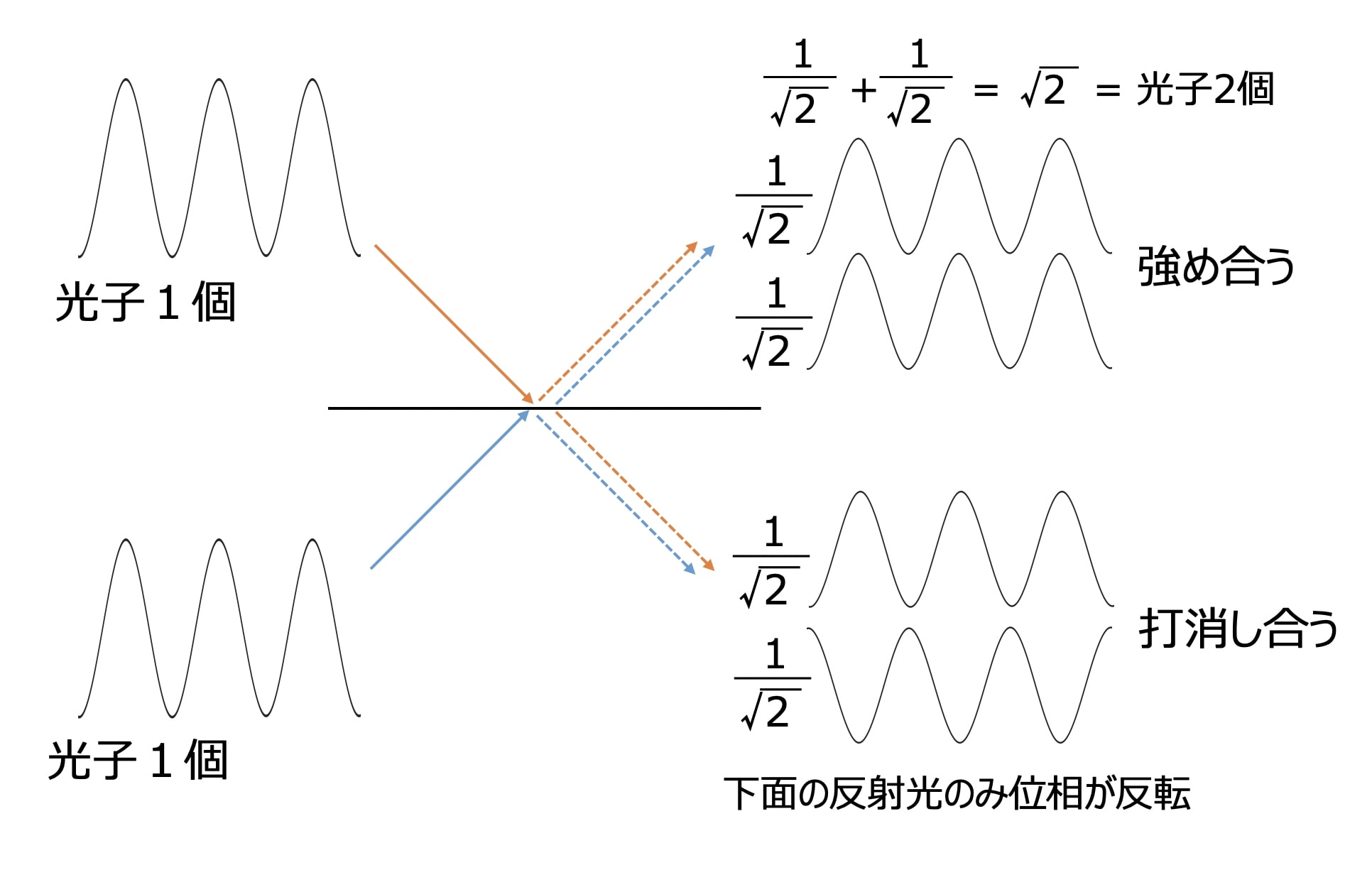
まず、下図のようにビームスプリッター(BS)の両側から同時に光子1個を入射する場合を考えてみます。
半分が透過し、半分は反射するため、図のように2つに別れるはずです。
まずBSの上面を見てみると、上面で反射した振幅(1/√2)の光と下面から透過してきた振幅(1/√2)の光が干渉し、振幅√2倍の光(光子2個)が出射されます。
次に下面では、下面で反射した振幅(1/√2)の光(位相が反転)と上面から透過してきた振幅(1/√2)の光が干渉し、打消し合って何も出射されないことになります。
(実際にこれは正しいのですが、正しいとすると光子1/2個という奇妙な状態が発生していることになりますが、結果としてそのような状態は現れないためOKのようです。)
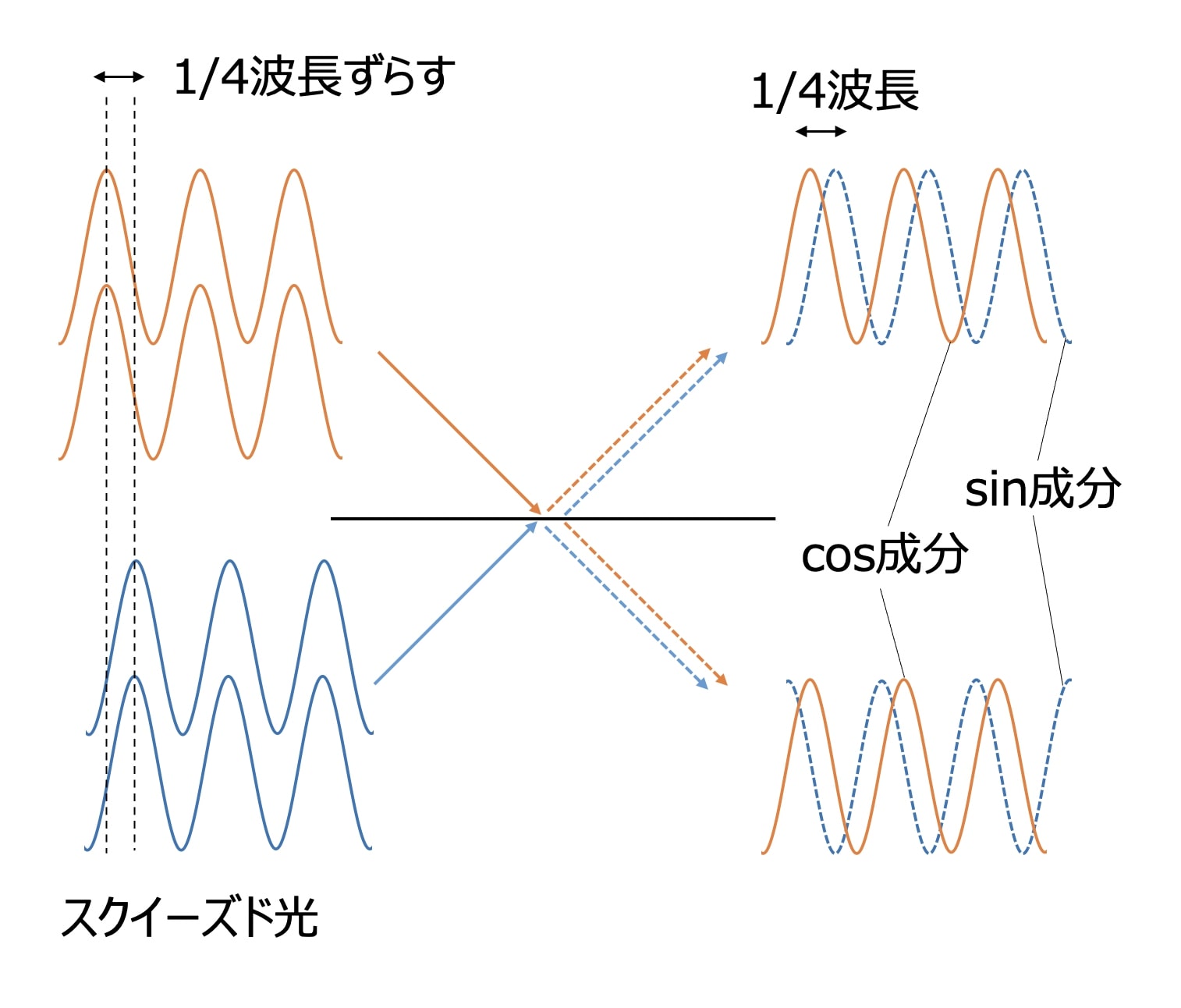
次に、BSの両側から入射する光の位相を1/4だけずらすと、出射光も位相がずれているため上図のような干渉を起こしません。
これを利用して、今度は下図のようにBSの両側から位相を1/4ずらした「スクイーズド光」を入射してみましょう。
スクイーズド光は光子2個がセットで飛んでくるため、出射光は振幅1の図の通りの関係になります。
これは、sin成分の和 = 0 、かつ cos成分の差 = 0 となり、さらに空間的にも分離できているためEPRペアであることがわかると思います。
以上がEPRペアの生成方法の一例です。
さいごに
実は3年ほど前から量子もつれについての解説を書こうと思っていたのですがなかなか書けていませんでした。
ここに書いたような内容を数式を使って説明すると非常に高度になってしまうのですが、図と言葉で説明すれば多くの人に理解できるのではないかと思い工夫して書いたつもりです。
(とはいえ難しいと思いますが)
量子力学はまだまだこれから新たな発見や新技術への応用がされていく分野であると思いますし、現象としても非常に興味深いものばかりです。
個人的には、現在の科学の常識は100年後、1000年後には全く別ものになっているだろうと思いますし、未知のテクノロジーもまだまだたくさん出てくるだろうと思っています。